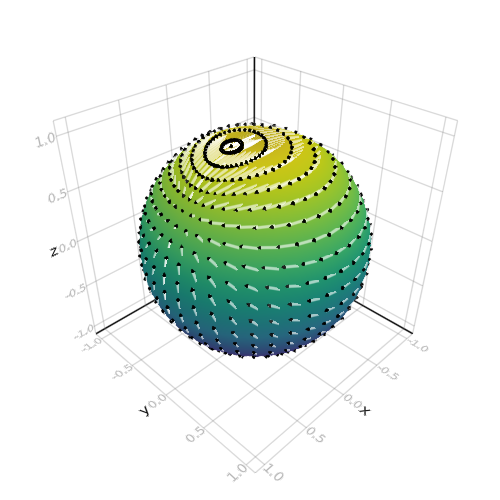
using LinearAlgebra using AbstractPlotting n = 20 f = (x,y,z) -> x*exp(cos(y)*z) ∇f = (x,y,z) -> Point3f0(exp(cos(y)*z), -sin(y)*z*x*exp(cos(y)*z), x*cos(y)*exp(cos(y)*z)) ∇ˢf = (x,y,z) -> ∇f(x,y,z) - Point3f0(x,y,z)*dot(Point3f0(x,y,z), ∇f(x,y,z)) θ = [0;(0.5:n-0.5)/n;1] φ = [(0:2n-2)*2/(2n-1);2] x = [cospi(φ)*sinpi(θ) for θ in θ, φ in φ] y = [sinpi(φ)*sinpi(θ) for θ in θ, φ in φ] z = [cospi(θ) for θ in θ, φ in φ] pts = vec(Point3f0.(x, y, z)) ∇ˢF = vec(∇ˢf.(x, y, z)) .* 0.1f0 surface(x, y, z) arrows!( pts, ∇ˢF, arrowsize = 0.03, linecolor = (:white, 0.6), linewidth = 3 )
